Эрлифты 

1. Общие сведения об эрлифтах 

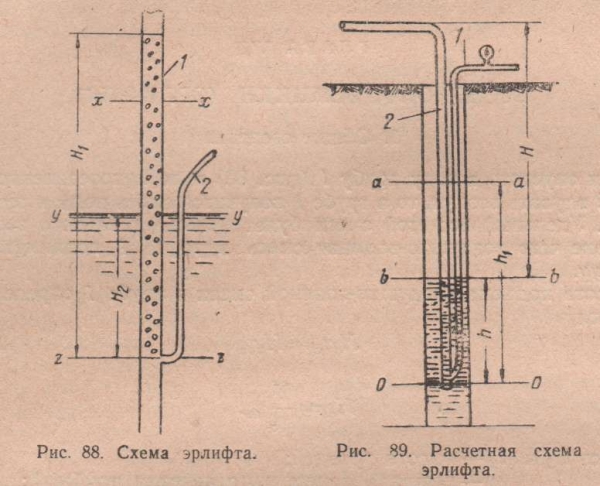
Если опустить в воду трубу 1 (рис. 88) и по присоединенной к ней трубке 2 вдувать воздух, то в трубе 1 получится смесь воды и пузырьков воздуха. Удельный вес этой смеси будет меньше удельного веса воды, вследствие чего воздушно-водяная смесь в трубе 1 поднимется выше уровня уу.

Высота подъема воздушно-водяной смеси в трубе 1 определится из уравнения. 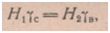 откуда 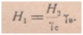. Здесь H1 и H2 — высота уровней;  - площадь поперечного сечения трубы 1; 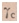 - удельный вес водовоздушной смеси;  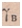- удельный вес воды. 

Для создания равновесия давления, действующие на площадь основания zz трубы как изнутри, так и снаружи, должны быть одинаковыми. Если срезать трубу 1 на высоте хх, то давление изнутри станет меньше, и поэтому под влиянием большего давления на дно трубы 1 со стороны окружающей ее воды смесь воды и воздуха начнет двигаться вверх и изливаться через разрез хх. Продолжая непрерывно вдувать воздух через трубку 2, можно получить непрерывный подъем воды вместе с пузырьками воздуха в трубе 1. 

Возможны два способа подъема воды. Можно вдувать воздух через большое отверстие. Воздух будет подниматься отдельными большими пузырьками и, как поршнем, выталкивать вверх воду. Можно вдувать воздух через мелкие отверстия, добиваясь возможно большего раздробления пузырьков воздуха, равномерно смешанных с водой. В водопроводном деле более широкое применение нашел второй способ впуска воздуха, на нефтяных же промыслах применяется первый способ. Впервые идея эрлифта появилась в самом конце XVIII в., во второй половине XIX в. были разрозненные попытки применения его, но только с 90-х годов прошлого столетия началось применение эрлифтов. 

2. Основные величины для проектирования эрлифтов 

На рис. 89 показана расчетная схема эрлифта. После начала действия воздухоподъемника статический уровень воды аа в скважине понижается и устанавливается динамический уровень на некоторой высоте bb. Высоту подъема воды над динамическим уровнем H; глубину погружения воздушной трубки 1 от уровня bb до места впуска воздуха в подъемную трубу 2 обозначим через h, а от уровня аа — через h1. В момент пуска эрлифта давление воздуха (измеряемое в метрах водяного столба) должно быть несколько более h1 когда же работа насоса установится, давление воздуха упадет до величины, немного большей h. Манометр, установленный на трубке 1, покажет это изменение давления. 

3. Глубина погружения 

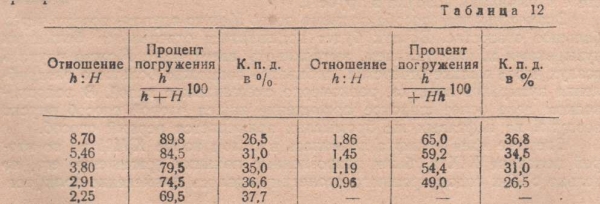
Отношение глубины погружения ко всей высоте подъема h:Н имеет большое значение для работы воздухоподъемника. Это отношение часто применяется в другой форме h:(h+Н); в этом случае погружение выражается в виде доли общей высоты подъема и погружения и представляется в процентах погружения. Из табл. 12 видно, как велико влияние этого фактора на к. п. д. эрлифта. 

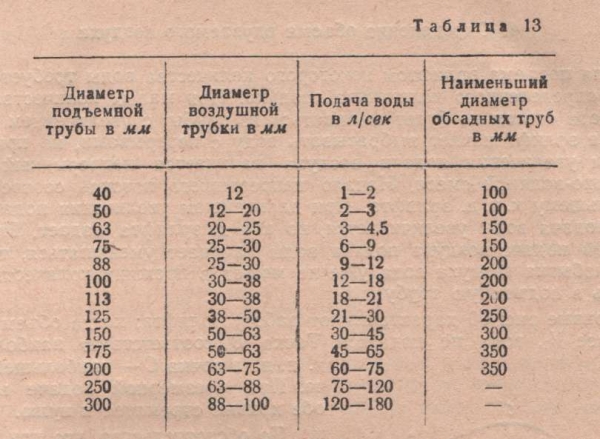
Для расчета водоподъемной трубы можно пользоваться практическими данными, приведенными в табл. 13. Эти цифры даны при 70% погружения. При меньшем проценте погружения подача уменьшается следующим образом: для 60%—на 12%, для 50 —на 22 и для 40% — на 40%.  

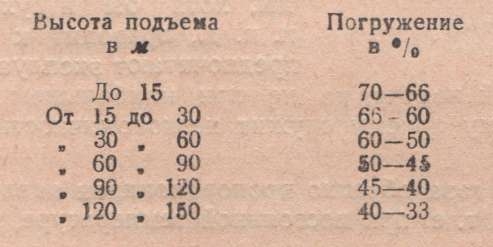
Наивыгоднейший процент погружения различен при разных высотах подъема. При определении процента погружения можно руководствоваться следующими данными: 

Для установления эрлифта скважина должна быть значительно глубже уровня воды в ней. Чтобы столб воздушно-водяной смеси Н + h (рис. 89) мог быть уравновешен столбом воды hi, необходимо, чтобы глубина погружения трубы 2 в воду имела достаточную величину, причем тем большую, чем больше высота подъема H. Но столб смеси воздуха я воды должен быть не только уравновешен: ему должно быть сообщено еще движение. Поэтому глубина погружения h должна быть еще больше, чем необходимо для гидростатического равновесия обоих столбов. 

Требуемая глубина скважины определяется из уравнения 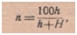, где n  - процент погружения, выбираемый соответственно требуемой высоте подъема. В этой формуле одно неизвестное — h, так как H определяется при пробных откачках. Практически глубина погружения водоподъемной трубы, а следовательно, и глубина скважины принимается от 1,5 до 3,0 H (n=40÷70%). 

4. Определение объема вдуваемого воздуха 

Для подъема эрлифтом некоторого количества воды требуется вдувание определенного количества воздуха. При малых количествах воздуха вода совсем не будет выливаться из трубы; с увеличением подачи воздуха эрлифт начнет выбрасывать воду с перерывами, но при дальнейшем увеличении подачи воздуха начинается непрерывный поток воздушноводяной смеси. Начало непрерывного потока соответствует наибольшему к. п. д. эрлифта. 

При дальнейшем увеличении подачи воздуха подача воды увеличивается, но к. п. д. эрлифта падает. При еще большей подаче воздуха подача воды начинает уменьшаться, так как из-за избытка воздуха вода уже не может в прежних количествах поступать в подъемную трубу. Кривые рис. 90 характеризуют работу эрлифта; когда объем воздуха менее V1, вода не подается. Точка В соответствует наибольшему к. п. д., а точка С — наибольшей подаче. При чрезмерной подаче воздуха обе кривые стремятся к нулю.  

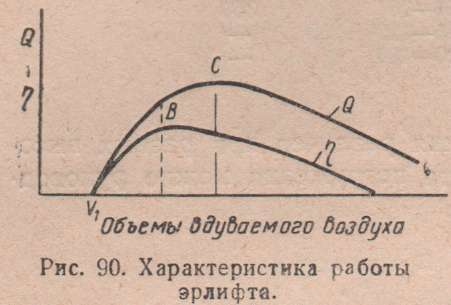
То обстоятельство, что при наиболее выгодном к. п. д. скважина не дает наибольшего количества воды и что, вдувая в скважину несколько больше воздуха, можно увеличить подачу воды, хотя бы и ухудшив при этом к. п. д., приводит к тому, что часто предпочитают эксплуатировать скважины при наибольшей подаче, но не при наибольшем к. п. д. эрлифта. Оправданием такому приему служит неэкономичность устройства глубоких скважин. 

Так как объем газа обратно пропорционален давлению при изотермических условиях, т. е. при постоянной температуре, то 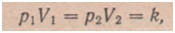 следовательно, работа, затрачиваемая на сжатие газа при изотермических условиях, равна  

Это выражение и представляет собой энергию воздуха, сжатого от атмосферного давления р1 до давления р2. Под таким давлением воздух подводится к низу подъемной трубы, где он имеет указанный запас энергии. Производимая сжатым воздухом полезная работа заключается в подъеме количества воды Q на высоту H (рис. 89) и равна QH. Отношение полезной работы ко всей затраченной работе представляет собою к. п. д. 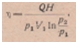 где p1 — атмосферное давление; V1 — требуемый объем воздуха при атмосферном давлении для подачи количества воды Q.  

Отсюда можно определить V1 — искомый объем воздуха: 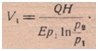 Если выразить р2 в метрах водяного столба, то оно будет равно h + 10, т. е. глубина погружения h + атмосферное давление равна 10м, a p1 = 10м. 

Разделив обе части на Q, получим объем воздуха при атмосферном давлении, требуемый на один объем поднятой воды при данном к. п. д; 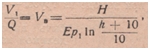. где Р1 — атмосферное давление (при VBB М3 И H В М) —должно быть выражено в т/м, т. е. Р1 = 10 т/ж2. 

При переходе от натуральных логарифмов к десятичным надо p1 умножить на 2,3; таким образом, получим .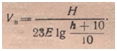  

Значение Е (к. п. д.) изменяется при разных процентах погружения — от 62 до 37% и ниже. Заменив 23Е общим коэффициентом С, получим 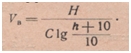. При разных процентах погружения коэффициент С (в метрических мерах) изменяется следующим образом (табл. 14). 

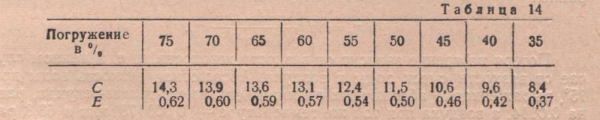
Из этой таблицы видно, что с уменьшением процента погружения падает к. п. д., а так как для глубоких скважин рекомендуются низкие проценты погружения, то очевидно, что с увеличением высоты подъема, т. е. глубины скважины, к. п. д. падает. При высоте подъема, например, в 30 м процент погружения равен 55 и соответствующий ему к. п. д. равен 0,54; при подъеме в 120 м процент погружения равен 40 и к. п. д, — 0,42.